PLANSITE-------SITEMAP----

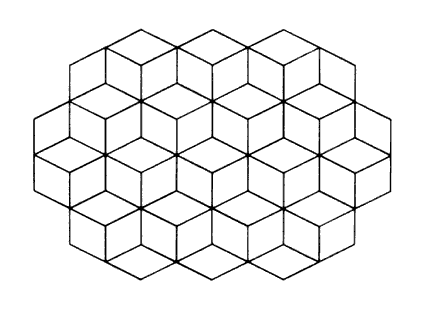
Plein ou creux, concave ou convexe, plongée ou contre-plongée, nous serions bien en peine de choisir l'une de ces occurrences en contemplant ce tracé noir sur le trottoir bitumé à la française. Et quand bien même aurions-nous, attiré par le logotype d'une entreprise de télécommunications française, reconnu l'ombre portée d'une cabine téléphonique, que nous serions toujours bien en peine de choisir parmi les branches des alternatives proposées.
Car l'hexagone d'ombre paraît tout autant être le sol creux et concave de la cabine que son sommet plein et convexe. Pour nous décider, nous devons entamer une réflexion qui, menée à son terme, permettra de circonscrire l'ambiguïté qu'avait fait naître une perception hâtive.
Ainsi, en premier lieu, le logotype déjà évoqué permet de donner un sens (une direction) à cette ombre et, en cela, de lui attribuer une signification : nous voyons l'ombre portée du sommet de la cabine. En second lieu, nous aurions pu avant ce premier constat, parer au plus pressé, en nous rappelant que le sol d'une cabine ne peut projeter une ombre au sol. Pourtant, en dépit de la connaissance et de la reconnaissance d'une cabine téléphonique, de la perception de son orientation, ce tracé sombre passe encore du creux au plein. Je peux, encore et toujours, m'imaginer en train de marcher sur l'hexagone foncé pour fouler le sol d'une cabine ouverte.

Cette image montre la force de figures aussi simples que les Cubes isométriques. Ainsi, dans la figure présentée ci-dessous, les différents volumes n'arrêtent pas de passer du concave au convexe sans que rien ne puisse les arrêter et figer notre vision en une image univoque.

Certains seront cependant amenés à penser que la photographie n'est pas si éloignée de l'illusion présentée, en ce que, l'ombre de la cabine s'apparente à un dessin tracé sur la surface plane du bitume. En cela, ces même personnes pourraient croire que l'illusion du concave et du convexe ne concerne que les deux dimensions de l'image. Afin de chasser cette idée de leur esprit et de montrer à tous que cette problématique concerne aussi les trois dimensions du réel, voici un lien qui vous conduira à une sculptures de Roy Lichtenstein :

https://www.youtube.com/watch?v=V3Xe70oqMDA

Qu'est-ce que je vous avais dit !

RETOUR AU SOMMAIRE

RETOUR À L'ACCUEIL