PlanDuSite-------SiteMap-----

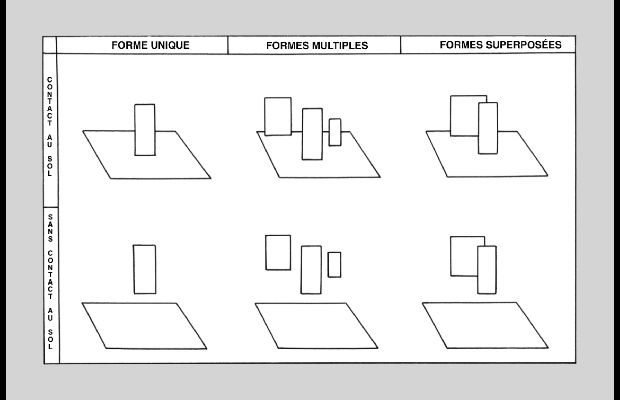
Pour comprendre le rôle des lignes des bases, nous allons, grâce au tableau n° 18, envisager les différentes positions d’un rectangle par rapport au plan du sol. La colonne gauche met en scène les deux relations spatiales qu’un polygone unique peut entretenir avec le sol. Alors que l’image supérieure affecte une position précise à son rectangle, nous sommes incapables d’évaluer sa place dans la rangée inférieure. Ainsi, en l’absence du contact au sol, toute forme quelle qu’elle soit serait déjà ambiguë, d’une ambiguïté singulière et universelle. Universelle, car le contact au sol paraît nécessaire à l’appréciation de tout échelonnement. Singulière, puisque nous avons là une nouvelle catégorie de l’ambigu, qui, au lieu d’offrir une vision alternative : le contact au sol ou son absence, nous propose une infinité d’interprétations. Faute de repères, le polygone inférieur peut en effet se situer à une multitude d’endroits différents. Bien que cette nouvelle catégorie de l’ambigu se passe du faux contact, de la superposition inversée et de l’alignement équivoque, elle s’attaque comme eux à l’échelonnement des formes dans l’espace. Il existerait donc une ambiguïté ordinaire du contact au sol, distincte des faux recouvrements, et nous aurons à en tenir compte dans notre classification générale. Mais, avant d’en arriver là, poursuivons par l’ambiguïté du contact au sol des formes multiples.

La colonne suivante présente trois rectangles échelonnés dans l’espace. Si l’image supérieure rend compte de la taille, de l’éloignement et de la situation réciproque de ces plans, la suivante, par l’absence du contact au sol, nous fait perdre toutes ces informations. En effet, cette image ne permet plus de connaître le rectangle le plus proche et le plus éloigné, ni de juger de leur taille respective ou des distances qui les séparent. Pire encore, nous avons maintenant l’impression d’être en face d’une double ambiguïté. La première, que nous venons de découvrir précédemment, perturbe la vision du rapport au sol de chaque rectangle, tandis que la seconde gêne la lecture des relations qui organisent leurs rapports spatiaux. L’une s’intéresse à la position individuelle des éléments dans l’espace, tandis que l’autre s’attache à leur position spatiale réciproque. Mais, bien que s’appliquant à des objets de nature différente, ces deux types d’ambiguïté produisent le même effet : que ce soit par l’absence du contact au sol ou par celle du contact entre éléments, nous sommes amenés à imaginer une infinité de positions différentes entre deux formes.

La troisième colonne s’intéresse quant à elle à des formes superposées. L’image supérieure présente deux rectangles partiellement recouverts, qui nous sont connus dans leur taille, leur éloignement et leurs relations réciproques. Pourtant, le recouvrement n’est pas essentiel, puisque l’image supérieure de la colonne précédente fournissait les mêmes informations. Le recouvrement ne fait donc que confirmer l’échelonnement donné par l’étagement des bases des plans à la surface du sol. L’image inférieure se distingue en revanche de sa voisine de gauche, en ce que l’absence du contact au sol ne nous prive plus de la totalité des informations spatiales. Si nous sommes incapables d’évaluer la distance séparant les plans et leur taille respective, le recouvrement persiste à nous signifier leur échelonnement réciproque. Ainsi dans le ciel, le recouvrement reste, avec les ombres portées, un des seuls indices permettant d’évaluer la situation réciproque des objets. Mais, ce principe de rendu de la profondeur ne suffit pas à supprimer toute l’ambiguïté d’une figure ordinaire. En effet, la dernière image n’est d’aucune utilité, lorsqu’il s’agit d’évaluer la distance entre les plans, ou ne serait-ce que de distinguer leur contact ou leur séparation. Ainsi, en l’absence de contact au sol, une superposition ordinaire est déjà ambiguë, de cette ambiguïté particulière qui nous fait hésiter entre une infinité de positions possibles.

Ce tableau nous aura donc appris des choses essentielles sur l’ambiguïté du contact au sol. En premier lieu, en l’absence de sol ou de son contact, tout élément se retrouve dans une situation spatiale ambiguë par l’incapacité que nous avons à le situer dans l’espace. En second lieu, deux éléments quels qu’ils soient, en l’absence de sol, d’un contact au sol marqué ou d’un contact réciproque, sont dans une relation réciproque ambiguë. Ce qui nous donne la règle suivante : en l’absence de contact au sol, toute relation spatiale entre une forme et son espace, ou deux formes séparées, est ambiguë. Ces deux ambiguïtés sont ordinaires, en ce qu’elles s’appliquent à toute forme dont la relation au sol n’est pas marquée. Ainsi, les trois figures de la rangée inférieure du tableau n° 18 constituent trois exemples différents de cette nouvelle branche de l’ambigu que nous appellerons : “ambiguïtés ordinaires”. D’un côté, nous aurions les ambiguïtés extraordinaires, qui nécessitent des éléments et des relations plastiques particuliers pour atteindre à l’équivoque, et de l’autre, les ambiguïtés ordinaires, applicables à toute forme, qu’elle soit unique ou multiple, dépourvue d’une relation au sol précise. D’un côté donc, le contact, la superposition et l’alignement seraient des relations plastiques permettant d’aboutir à des conflits spatiaux extraordinaires en ce qu’ils remettent en cause l’évidence du contact au sol ou des relations spatiales entre les éléments, tandis que de l’autre, l’absence du sol ou de son contact déboucherait sur des ambiguïtés ordinaires en ce qu’aucune forme particulière et qu’aucune relation plastique spéciale ne seraient requises pour qu’un élément subisse leur perte.

Mais, cette nouvelle branche de l’ambiguïté possède une deuxième particularité, qui permet encore de la distinguer des ambiguïtés extraordinaires. Qu’elles concernent la position d’un élément unique dans l’espace ou les relations réciproques d’éléments différents, les ambiguïtés ordinaires offrent un nombre infini de situations spatiales différentes. Pour cette raison, nous dirons des figures, qui possèdent la particularité de nous faire hésiter entre une multitude d’échelonnements individuels ou réciproques, qu’elles présentent des ambiguïtés infinies, et de celles, qui n’utilisent que quelques dispositions précises pour fonder leur équivocité, qu’elles offrent des ambiguïtés finies. Pourtant, malgré ce que nous venons de dire et ce que nous pourrions croire, les ambiguïtés infinies ne sont pas réservées aux ambiguïtés ordinaires, de même que les ambiguïtés finies ne sont pas liées aux ambiguïtés extraordinaires. En effet, lorsqu’une contiguïté, une superposition ou un alignement, s’établit entre les différents éléments d’une figure impossible ou ambiguë, les ambiguïtés infinies viennent s’intercaler entre les ambiguïtés finies réciproques. Ainsi, nous ne connaîtrons jamais la distance qui sépare les deux branches de la Tripoutre inversée (voir les Variations de la Tripoutre). De même, avant de lever l’ambiguïté infinie des trois rectangles de la rangée inférieure du tableau n° 18 en estimant leur distance réciproque, nous pouvons déjà lever leur ambiguïté finie en leur attribuant un rang hypothétique.

Le tableau n° 18, nous aura permis de découvrir les ambiguïtés ordinaires, en même temps que de nouvelles caractéristiques : les ambiguïtés finies et infinies. Mais, ce tableau permet aussi de réaffirmer l’importance des lignes de base des formes. Pourtant, en tant que maillons plastiques d’une chaîne de production du sens, ces dernières ne sont rien en elles-mêmes. Nous avons donc à trouver le réseau de significations auquel ces lignes participent pour fonder l’ambiguïté des images.

RETOUR AU SOMMAIRE

RETOUR À L'ACCUEIL