|
AVERTISSEMENT
Depuis que Wikipedia et Wikimedia Commons considèrent que la Tripoutre de Roger Penrose (plus souvent appelée Triangle de Penrose ou triangle impossible) relève du domaine public, je me permets de mettre en ligne ce tableau réalisé en 1999, et qui, pour des raisons supposées de droits d'auteur, n'avait pas jusqu'alors été publié sur le site.
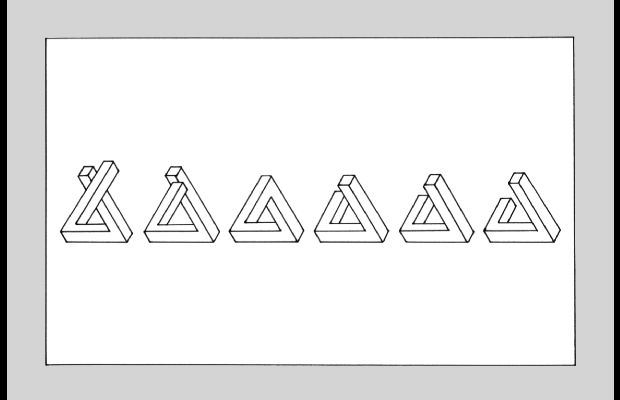
Nul besoin d'être un spécialiste des figures impossibles pour comprendre que nous avons là des variantes de la Tripoutre. Ces variantes sont rangées de gauche à droite afin de nous faire progressivement passer du domaine de l'impossible à celui du possible.
Les habitués du site, tels que le webmestre, savent depuis longtemps que l'impossible et l'ambigu sont des domaines contigus et continus et qu'il suffit de bien peu de chose (parfois une ligne, parfois un espace ou une simple contiguïté graphique) pour basculer de l'un à l'autre. Mais, le tableau n° 7 rend compte des impossibilités et des ambiguïtés d’une figure unique. Car la Tripoutre et ses variantes réunissent en un ensemble unique, continu et solidaire, trois éléments discrets. À ce titre, le tableau n°7 propose une classification des faux échelonnements des figures uniques. Abordons maintenant les différentes catégories en partant de la première figure à gauche (fig. 1) pour terminer par la sixième à droite (fig. 6).
FIG. 1 La Tripoutre à superposition inversée.
En tant que superposition inversée par outrepassement, la figure n° 1 présente un dépassement en longueur et en profondeur de la poutre gauche sur celle de droite. Avec cette première figure, la superposition inversée relève d'un évident outrepassement en profondeur de la droite, outrepassement que nous pourrions qualifier de faux recouvrement. Le recouvrement des formes étant le système le plus simple et le plus ancien de rendu de la profondeur, qui permet d'obtenir un échelonnement des plans dans la profondeur ainsi suggérée de l'espace.
FIG. 2 La Tripoutre à superposition inversée et contact impossible
La figure n° 2, qui s'arrête avant que le chevauchement des poutres ne soit consommé, est une superposition inversée, mais une superposition inversée qui nous donne le sentiment d'être en face d'un contact impossible. En annulant le dépassement, le raccourcissement de la barre gauche arrive presque à faire oublier l’outrepassement en profondeur par la contiguïté que nous imaginons alors entre les poutres. Nous atteignons ainsi un seuil, puisque cette figure nous fait hésiter entre deux interprétations impossibles : une superposition inversée et un faux contact. D'un côté, les directions prises par les deux poutres obliques, nous font comprendre que nous sommes devant une superposition inversée. De l’autre, l’absence de dépassement et la faiblesse de l’outrepassement en profondeur nous poussent à faire de cette figure un contact impossible. Cette ambiguïté des interprétations provient de l’équivocité du contact. Nous avons là une superposition inversée à contact ambigu.
FIG. 3 La Tripoutre de Penrose
Que dire de la Tripoutre de Penrose, encore appelée Triangle impossible ou Tribar, qui n'ait déjà été dit. Je me permets cependant de vous conseiller la courte page consacrée à la Tripoutre de Penrose sur ce site, page qui vaut surtout pour les liens situés en bas de page.
FIG. 4 La Tripoutre à contact équivoque de surfaces.
La figure n° 4 nous fait entrer dans le domaine de l'ambigu. Car si un recouvrement normal échelonne les poutres dans l’espace, l'enchaînement logique des figures nous permet d’imaginer une contiguïté des poutres. Ainsi, nous voilà de nouveau confrontés à une ambiguïté du contact. Mais, au lieu d’opposer les deux lectures impossibles de la superposition inversée, ce contact ambigu nous fait hésiter entre une vision possible et une autre impossible d'un recouvrement ordinaire. À supposer la séparation des poutres, nous avons une figure possible et ouverte, et à imaginer leur contiguïté, nous obtenons une figure impossible fermée. Mais ici, le possible triomphe. Il nous est plus facile d’imaginer un écart entre les poutres qu’un contact. Ainsi, grâce au renversement du recouvrement des poutres, nous sommes passés d'une impossible ambiguïté (fig. 2), à une possible ambiguïté (fig. 4). Mais, nous réalisons maintenant que l’ambiguïté peut naître d'un recouvrement normal. Ainsi, tous les recouvrements, qu'ils soient vrais ou faux, peuvent, à certaines conditions, être perçus de manière ambiguë. Avec cette figure, nous avons donc ce que nous appellerons un contact équivoque de surfaces. Bien que son dessin puisse apparaître banal, logique et évident, nous verrons plus avant que cette image fait partie d'une catégorie d’ambiguïté distincte, originale et à part entière. Abordons maintenant les alignements.
FIG. 5 La Tripoutre à contact équivoque de contours.
L’alignement ambigu pose, quant à lui, moins de problèmes. En effet, faute de contact de surfaces et de superposition inversée, les deux figures que nous avons conservées délaissent peu à peu l’impossible. Pourtant, à la manière de la figure précédente, nous hésitons toujours entre la contiguïté et la séparation des poutres. Ainsi, à imaginer une simple coïncidence de contact des poutres, nous aboutissons à une séparation possible, tandis qu'à accepter la matérialité du contact des arêtes, nous obtenons un contact impossible. Ainsi, l’ambiguïté du contact est une nouvelle fois le pivot de cette figure. Mais, à la différence des deux précédentes ambiguïtés de contact, la contiguïté des contours remplace maintenant celle des surfaces. Ce qui ne change pas grand chose à notre perception de la figure, puisque ce contact d’arêtes, malgré sa fragilité, nous pousse encore à rapprocher les deux poutres que nous savons distantes. Nous aurions donc là un contact ambigu de contours. Malheureusement, cette figure est plus complexe qu'il n’y paraît au premier abord.
C'est que le contact ambigu de contours se double d'un alignement équivoque des arêtes et des plans. Malgré un écart réel et visible, la section de la barre droite semble se situer dans le prolongement de la face supérieure de la gauche. Cet alignement participe à l’interprétation impossible de cette figure. L'addition du contact ambigu et de l’alignement équivoque, nous incite à imaginer un faux contact. Seule cette accumulation arrive à expliquer que le plateau de la balance de l’ambiguïté puisse parfois pencher du côté de l’impossible.
Mais pour lors, une question se pose : est-ce-que le contact ambigu de contours serait encore viable en l’absence de l’alignement équivoque des plans ? Bien sûr, car à prolonger la poutre droite de cette figure, nous serions toujours dans l’ambigu sans que l’alignement ne se manifeste.
FIG. 6 La Tripoutre à alignement équivoque.
La figure n° 6 est, quant à elle, beaucoup plus simple. Ici, plus de superposition inversée ou de contiguïté de surfaces ou de contours, pour nous égarer. Ainsi, en l’absence de toutes ces relations spatiales, la séparation des poutres est consommée. Pourtant, l'alignement ambigu peut encore nous tromper. Même si nous savons que les deux branches de la Tripoutre sont distantes, l’alignement des deux poutres instille encore l’ombre d'un doute dans nos esprits. C'est en cette variante de la Tripoutre que l’impossible prolongement des poutres obliques est le moins acceptable.
Premier constat.
La Tripoutre étant à l'origine de toutes ces variantes, nous pouvons supposer que toute figure impossible ou ambiguë unique pourra, après modifications, produire des variantes impossibles ou ambiguës de son propre modèle. Les manipulations de la Tripoutre nous ouvrent ainsi les portes d'un système de production des figures impossibles et ambiguës. Ce système de production peut s'expliquer par le fait que les catégories présentées ne sont pas des entités autonomes, mais le résultat d'une logique plastique.
Deuxième constat.
À parcourir le tableau n° 7 de la gauche vers la droite, nous voyons la logique plastique de manipulation des figures uniques. Le passage d'une figure à l’autre se fait par le raccourcissement progressif et gradué de la poutre gauche. Ce raccourcissement permet à la poutre droite de s'avancer peu à peu au premier plan, en nous faisant passer par les différentes catégories de l'impossible et de l'ambigu. Mais, ne nous méprenons pas : ce détail n’explique pas l’impossible et l’ambigu, il représente seulement le moyen plastique qui en actualise les effets.
Troisième constat.
La Tripoutre est un élément structurel central de l'impossible et de l'ambigu des figures uniques, Grâce à elle, nous arrivons à retrouver et à catégoriser l’ensemble des figures uniques. Ainsi, à gauche, l’outrepassement du contact permet d’atteindre les différentes superpositions inversées, tandis qu’à droite, son délaissement aboutit au contact équivoque puis à l’alignement ambigu. Le contact incohérent de la Tripoutre marque donc la limite entre le contact outrepassé et le contact délaissé. L’outrepassement et le délaissement étant deux formes particulières et distinctes de la perte du contact, nous pouvons aussi les comprendre comme des séparations. Alors, à formuler les choses autrement, tout se jouerait, ici comme dans la vie, entre le contact et la séparation.
Si Penrose Junior a eu le bon goût d'inventer la Tripoutre ou Triangle impossible, son père a répondu à sa question imagée par un Escalier impossible. Vous pourriez donc être intéressés par ces trois pages : Escaliers impossibles connus, méconnus, dessinés ou encore photographiés dans la nature !
RETOUR AU SOMMAIRE
RETOUR À L'ACCUEIL
|
|