|
|||
 |
|||
 |
|||
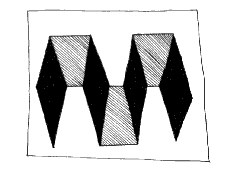
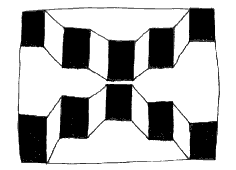
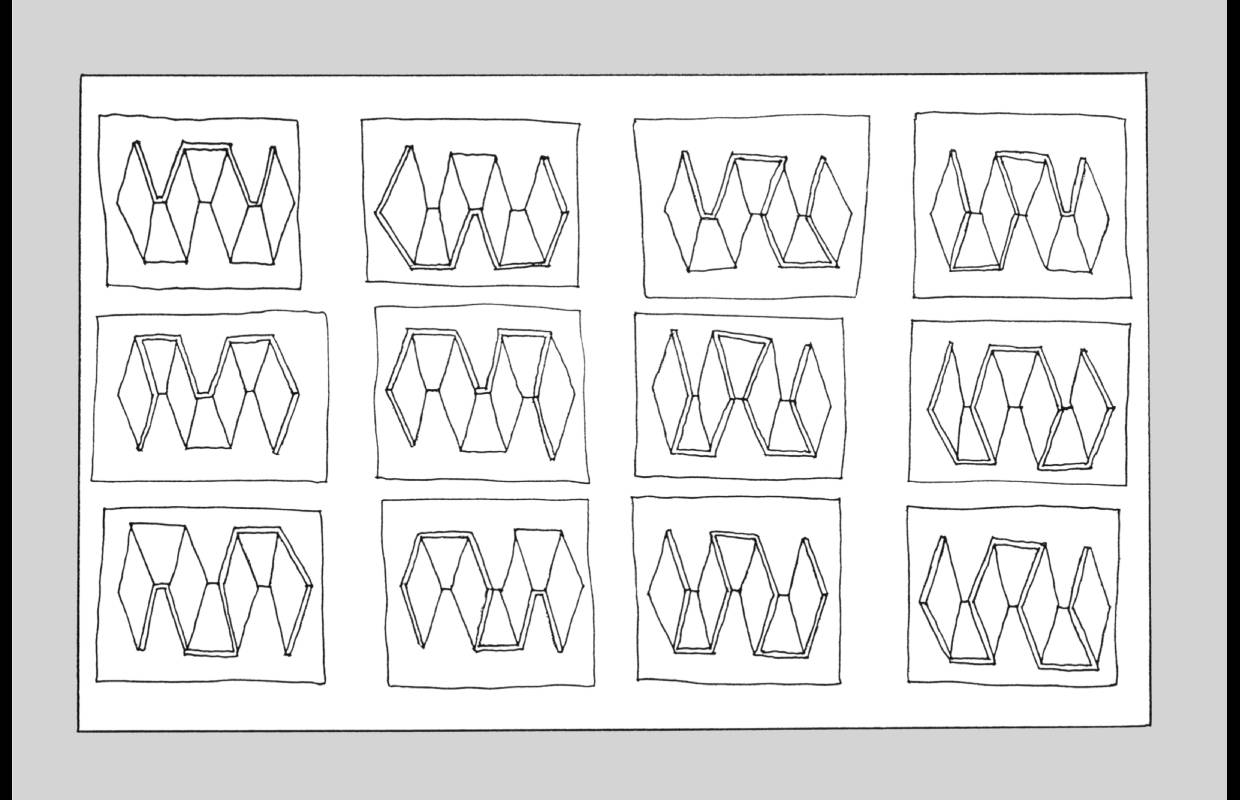
La figure C4 ( ci-dessous à gauche) est un bande pliée qui oppose, en un premier temps, une vision pleine à une autre creuse, en même temps que la plongée à la contre-plongée. Cette opposition ne suffit pourtant pas à rendre compte de la totalité des visions. Le tableau n° 26, présenté ci-dessus et conçu à l’époque de la réalisation de cette figure, recensait déjà 12 interprétations différentes, qui, du fait d’un dénombrement non mathématique, ne prétendent pourtant pas à l’exhaustivité. Essayons de comprendre les raisons de cet accroissement des interprétations alors que le nombre de plans de cette figure est largement inférieur à celui de la figure C3 du tableau n°25 (ci-dessous à droite).
Pour cela, nous avons à découper l’image en modules. Un module se compose de trois plans : deux parallélogrammes associés à un trapèze central. À l’instar de la figure C3 du tableau n°25, le module offre une vision pleine et une autre creuse. Mais, à sa différence, il permet encore d’imaginer des visions latérales complexes combinant diverses orientations. Les deux parallélogrammes du module peuvent s’orienter vers la droite, puis vers la gauche, ou encore diverger et converger. Un module autorisant quatre orientations, sa combinaison avec l’autre débouche sur un minimum de 16 interprétations. Mais, ce ne sont pas tant les parallélogrammes qui conduisent à ce résultat, que leur liaison avec des trapèzes. En effet, la figure C3, qui réunissait ses parallélogrammes par des rectangles, ne permettait ni divergence, ni convergence, et encore moins leur alternance. Le trapèze ajoute donc ses propres ambiguïtés à celles des parallélogrammes. Ainsi, pour une vision d’un parallélogramme, nous obtenons deux positions du trapèze : ce dernier peut rester à la verticale pour fermer le fond de la figure, ou s’incliner afin de former le toit des parallélogrammes. En revanche, un rectangle subit des variations d’échelonnement sans que son orientation en soit pour autant beaucoup modifiée. Mais, ce ne sont pas tant les formes que les lignes qui sont en cause. À cause de ses verticales, un rectangle ne peut s’orienter que dans une seule direction principale, alors que le trapèze contient des obliques, qui peuvent tout autant se dresser vers le ciel que s’éloigner sur le sol. Ainsi la liaison des parallélogrammes est plus ambiguë lorsqu’elle est opérée par de trapèzes, car les verticales disparaissent pour laisser la place aux obliques. Enfin, si l’on accepte qu’un module central vienne se superposer en partie aux latéraux, cette figure comporte au total trois modules. Mais, les bandes pliées pouvant se poursuivre à l’infini, chaque module ajouté devrait multiplier par quatre le nombre des interprétations. Nous retrouvons là l’indénombrable des ambiguïtés finies. Car, à poursuivre l’enchaînement des modules, nous atteignons très rapidement un nombre quasi infini de dispositions réciproques des différents modules. Mais, là encore une formule mathématique pourrait être établie qui devrait permettre de calculer cet indénombrable qui n’a d’infini que son aptitude à dépasser les capacités interprétatives de notre système visuel. Voilà, nous en avons terminé avec les figures personnelles à superposition équivoque.
|
|||