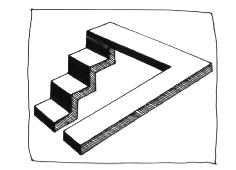PLANSITE-------SITEMAP----

ANALYSE : "Croquis B1 du tableau 34 "

Si les deux figures précédentes opposaient l’orientation de leur surface à l’échelonnement de leurs dents, nous en arrivons à des images qui semblent privilégier les conflits d’échelonnement. En effet, les Escaliers alignés (fig. B1 et B2, tableau 34) donnent le sentiment qu’à gravir leurs marches nous nous retrouverions au niveau de notre point de départ. La figure B1 nous fait ainsi souvenir de l’Escalier de Penrose. Pourtant, le passage de l’impossible à l’ambigu nécessite une modification d’importance, qui est l’ouverture. Nous avons maintenant une figure ouverte, qu’il conviendrait de fermer en ajoutant un quatrième élément reliant la première marche à la fin de l’escalier pour revenir à un véritable faux contact. Nous aurions alors une figure fermée, variante à une volée de l’Escalier de Penrose. Mais, l’ouverture de cette figure interdit l’impossible, et, à la place, nous avons un alignement équivoque, qui, grâce au principe de colinéarité, donne l’illusion de la fermeture sans l’assurer. Cet objet pourrait donc être construit, et, sous un point de vue précis, ses deux extrémités sembleraient s’aligner, bien qu’elles fussent séparées dans la réalité. Nous retrouvons donc là une nouvelle figure impossible-possible, qui se laisse croire inconstructible alors qu’elle ne l’est pas.

Avec cette figure unique complexe, les contours sont encore les éléments fondateurs de l’ambiguïté. La colinéarité nous pousse à poursuivre les lignes qui expriment l’épaisseur du début et de la fin de la construction. Ces lignes, à moitié réelles et à moitié imaginaires, sont le support matériel de l’illusion, puisque leur tracé réunit sur un même plan deux surfaces éloignées. Ainsi, les deux lignes des épaisseurs des extrémités suffisent à aplatir l’ensemble de la construction. En cela, nous avons une ambiguïté de contours partiels. Mais, l’origine plastique de l’ambiguïté n’explique pas pourquoi nous aurions un conflit d’orientation avec la Scie (croquis précédent), et un simple conflit d’échelonnement avec cet Escalier aligné. Deux échelonnements s’offrent en effet à nous : nous pouvons imaginer les deux extrémités de l’escalier à un même niveau, ou les éloigner l’une de l’autre dans la hauteur de l’espace représenté. En fait, la Scie, ne possédant qu’un seul plan, était condamnée à échelonner une partie de sa surface, les dents, afin de contredire l’orientation générale de son volume. En revanche, les trois volumes de l’Escalier aligné, qui en font une figure unique complexe, lui permettent d’investir les trois dimensions de l’espace. Pour cette raison, ses trois masses semblent donner lieu à un conflit d’échelonnement, sans nécessiter l’appoint d’orientation conflictuelles.

Pourtant, cet échelonnement sort de l’ordinaire en ce qu’il s’attaque à la hauteur de l’espace, plutôt qu’à sa profondeur. En effet, à cacher de la main la partie inférieure de cette figure, nous voyons une déclivité, tandis qu’à masquer la partie supérieure, ses extrémités semblent se rejoindre. En fait, tout dépend du sens sous lequel nous regardons cette figure, puisqu’à retourner la page, la volée de marches, qui se dirigeait vers le haut, s’enfonce alors dans la profondeur de l’image. Vu sous cet angle, l’Escalier aligné ressemble maintenant à la Tripoutre alignée. Pour cette raison, l’orientation ne peut totalement être absente de cette figure. Car, pour qu’une figure unique puisse donner le sentiment de la continuité illusoire de ses extrémités malgré l’évidence de leur échelonnement, il faut que nous inventions une torsion, qui modifie l’orientation de ses éléments. Regardons l’Escalier suivant. Deux organisations plastiques peuvent s’y lire. La première oppose l’échelonnement en hauteur de la moitié gauche des marches à un échelonnement en profondeur de la partie droite. La seconde met en conflit l’orientation montante de la partie gauche et l’orientation horizontale de la partie droite. Là, nous voyons mieux combien orientation et échelonnement sont étroitement mêlés à l’intérieur des figures uniques et complexes qui ne font que reprendre la structure de la Tripoutre ou de l’Escalier de Penrose.

Enfin, pour en terminer, nous devons décider ce qui triomphe ici de l’aplatissement ou de l’approfondissement. Le premier Escalier aligné renie, par l’alignement de ses extrémités, la hauteur de sa volée de marches, tandis que le second, en raison de l’alignement du côté droit de ses marches, refuse l’élévation de sa moitié gauche. En ces deux figures, nous avons donc un aplatissement de la hauteur de l’espace. Mais, cette hauteur est particulière en ce qu’elle associe, comme pour tout escalier normal, un échelonnement en profondeur à une orientation montante. Ainsi, nous sommes loin de l’approfondissement illusoire du plan unique de la Scie. Cette situation s’explique par le fait que nous avons là des figures uniques complexes, en lieu et place d’un volume unique. Leur articulation particulière permet aux figures uniques complexes de remettre en cause l’échelonnement réciproque de leurs extrémités, en même temps que de bouleverser l’orientation de l’espace interne qu’elles se sont ingéniées à mettre en place. Elles se distinguent ainsi des figures uniques simples qui ne maltraitent que les masses.

ADDENDUM
Pour une analyse plus récente (fin 2011) de cet escalier, voir la page consacrée aux Escaliers impossibles personnels.

VOIR LE CARNET

Cliquez sur ce lien pour découvrir la double page du carnet où figure ce croquis. En feuilletant le carnet vers l'avant ou vers l'arrière, vous pourrez découvrir des variantes, qui, en tant que variantes mineures, n'ont pas été intégrées aux tableaux de la classification, et n'ont donc pas donné lieu à analyse.

RETOUR AU TABLEAU

RETOUR À L'ACCUEIL