|
AVERTISSEMENTS
J'affirme haut et fort que je n'ai lu aucun des livres cités en cette page (hormis La grammaire du voir dont j'ai tout oublié). Je ne peux donc certifier que les différents auteurs n'ont pas, à un moment ou un autre, évoqué les images présentées ici comme ayant été des sources possibles de leur croquis. De même, il convient de souligner que les appellations Figure de Untel n'émanent pas des psychologues étant à l'origine de la publication de ces figures, mais de personnes qui ont cru bon, pour la simplicité des débats scientifiques ultérieurs, de les nommer d'après le nom de l'auteur du livre dans lequel elles avaient été publiées, et ainsi, mises à l'honneur en même temps que portées à la connaissance de tous.
LA CAISSE IMPOSSIBLE
n'a pas découvert le Cube impossible ce détail d'une lithographie intitulée Belvédère, datée de 1958. Et a encore moins inventé la Caisse impossible, lorsqu'il en a publié le dessin dans un article intitulé : The Penrose triangle and a family of related pictures, Perception, 7, 1978, p. 283-296.
Bien que l'objet soit différent, le siège de ce souverain moghol exprimait depuis belle lurette une impossibilité spatiale similaire à celle de la caisse que nous voyons de nos jours dans n'importe quel livre ou site de vulgarisation consacré aux illusions d'optique. Pour lire l'analyse de ce détail d'une miniature indienne, dont j'ai malheureusement égaré la source, veuillez suivre le lien suivant : Le trône impossible.
  
MA FEMME ET MA BELLE-MÈRE
n'a pas découvert Ma femme et ma belle-mère, cette caricature parue sous son nom dans le journal satirique en 1915, et qui a connu la consécration en étant reproduite dans un article de : A new ambiguous figure, American Journal of Psychology, vol.42, n°3 juillet 1930, p. 444-445.
Des cartes postales allemandes de la fin du XIXème siècle utilisaient, pour leurs vertus prophylactiques et propitiatoires, ce procédé que les versions modernes, à travers une vision hygiéniste et soi-disant rationnelle des rapports hétérosexuels, se sont contentées d'édulcorer, perdant en cela le savoir coutumier accumulé au fil du temps par les générations passées.
Afin d'approfondir l'iconographie de cette image et trouver les liens et une bibliographie appropriés, allez sur :
http://mathworld.wolfram.com/YoungGirl-OldWomanIllusion.html
Pour voir l'original de Hill à la librairie du congrès :
http://www.loc.gov/pictures/item/2010652001/
  
LE DIÈDRE DE MACH
n'a pas découvert le Dièdre de Mach, dessin publié en 1886 dans : Beiträge zur Analyse der Empfindungen (traduction française de l'édition Gustav Fischer, Iena, 1922 : Analyse des sensations, éditions Jacqueline Chambon, Nîmes, 2000, p. 185 et 197).
Cette figure, connue depuis l'antiquité, a été utilisée dans toutes les civilisations. Je vous renvoie donc à une mosaïque romaine (ci-dessous à droite), au motif décoratif d'une colonne du Taj-Mahal, et enfin au célèbre parquet à point de Hongrie, dont je ne vous montrerai aucun exemple tant vous pouvez le trouver en de nombreux appartements parisiens pré ou post hausmanniens, et sur lequel il m'arrive parfois de tanguer.
  
LE CUBE DE NECKER
n'a pas découvert le Cube de Necker, dessin publié en 1832 dans : Observations on some remarkable phenomena seen in Switzerland; and an optical phenomenon which occurs on viewing of a crystal or geometrical solid, Philososphy Magazine, 1, p. 329-337.
Ce cube là traînait depuis fort longtemps, sous sa forme cavalière ou isométrique, en de nombreux décors de nombreuses cultures à diverses époques. Ainsi, la mosaïque d'époque romaine, présentée ci-dessous à droite, reprend-elle avant même de l'avoir connu, le principe bien connu du Cube de Necker. Pour ceux qui voudraient lire l'analyse de cette mosaïque antique.
  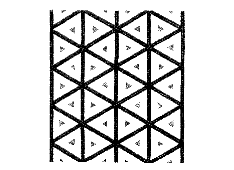
LA TRIPOUTRE DE PENROSE
Comme son nom ne l'indique pas, n'a pas découvert la Tripoutre de Penrose (image hors-site). Bien qu"il ait publié le dessin d'une Tripoutre dans un article du British Journal of Psychology, daté de 1958 et intitulé : Impossible objects: a special type of illusion, nous pouvons trouver des antécédents à cette figure.
, dans un entretien avec , raconte qu'il s'était amusé à créer des figures impossibles après avoir vu une exposition consacrée aux dessins d'. Pourtant, cette exposition ne présentait aucune Tripoutre puisqu' ne commença à s'intéresser et à utiliser cette forme qu'après avoir reçu l'article de . D'un autre coté, n'a eu connaissance de la Tripoutre d' qu'en 1984. Les postes suédoises avaient en effet rendu un hommage philatélique tardif (1982), à cette première Tripoutre imaginée et réalisée en 1934 (ci-dessous à gauche).
Mais, une autre influence pourrait êtres à l'origine du dessin de 1958. Je ne peux pas ne pas imaginer que le grand érudit qu'est Sir n'ait pas vu au moins une fois dans sa vie avant de brosser cette figure impossible, la gravure du célèbre peintre anglais où l'on aperçoit une enseigne (détail ci-dessous à droite), dont la potence n'est pas sans évoquer une Tripoutre avant la lettre. Je suppose, comme tout dessinateur qui se reconnaît comme étant une éponge à images, que a pu subir l'influence inconsciente d'une gravure précédemment vue et momentanément oubliée. Pour ceux qui voudraient lire l'analyse de la potence d'enseigne à la lune couchée, allez à la page : L'enseigne.
  
LA QUADRIPOUTRE DE DRAPER
n'a pas peut être pas découvert ce que j'appelle (en référence à la Tripoutre) la Quadripoutre, lorsqu'il en a publié le dessin dans un article intitulé : The Penrose triangle and a family of related pictures, Perception, 7, 1978, p. 283-296.
cite dans son livre Le monde des illusions d'optique (éditions Taschen, 1992, p.85) une oeuvre de , The magpie on the gallow, datant de 1568, où nous voyons au centre de l'image, une potence dont l'orientation dans l'espace en arrive à une impossibilité presque similaire à celle du dessin de .
  
LE TRIANGLE DE KANIZSA
a bien découvert le Triangle de Kanizsa. La première publication française de cette figure peut être trouvée dans un livre traduit de l'italien en 1997 : La grammaire du voir, Éditions Diderot, collection “Pratique des sciences”.
Mais, va jusqu'à citer la source graphique qui l'a inspiré : le Carré, dessin de publié en 1904 dans : Einige Beobachtungen uber die Zusammenfassung von Gesichtseindrucken zu Einheiten, Psychologishe Studien 1 1-32. Pourtant lorsque vous comparerez le Trapèze (variante non officielle et éhontée du Triangle) avec le Carré, vous comprendrez qu'il a fallu un travail de conceptualisation important pour deviner que ce petit carré stupide allait pouvoir donner lieu à de nombreux écrits, de multiples débats (pour lors non résolus) et une quantité quasi infinie de figures fictives (figures dont vous pouvez consulter de nombreuses variantes sur le site recommandé d'un individu fort recommandable que je me permets donc de vous recommander : http://figuresfictives.free.fr)
  
LE LAPIN-CANARD DE JASTROW
n'a certainement pas découvert le célèbre Lapin-canard, mais il en a à chaque fois cité les sources. Ainsi, tant en 1899 ( The mind's eye, Popular Science Monthly, 54, 299-312), qu'en 1900 (, Fact and fable in psychology, Boston, Houghton Mifflin), l'origine allemande de l'image (à gauche) est bien précisée. Pour tout savoir plus sur l'histoire mouvementée de cette image populaire et voyageuse, allez sur la page que j'ai abondamment pillée :
http://ist-socrates.berkeley.edu/~kihlstrm/JastrowDuck.htm
  
Voilà, c'est fini pour l'instant, mais il y a fort à parier que, à la manière des images montrées ici, d'autres figures, qui ont fait ou feront le buzz sur le web, risquent fort de na pas donner les sources historiques qui sont à l'origine des images proposées sur internet.
RETOUR AU SOMMAIRE
RETOUR À L'ACCUEIL
|
|
















