|
LA THÉORIE
N'importe quel étudiant en première année de psychologie de la perception doit savoir que les neurones ont des taches bien spécifiques à accomplir. Ainsi, tandis que certains se contentent de détecter les verticales et les horizontales, d'autres cherchent à repérer les contours ou encore les seuils de valeurs. Poussant leurs investigations au-delà des lignes, les chercheurs ont découvert que certains neurones étaient spécialisés dans la détection de formes bien particulières : les jonctions. Ces dernières, pour lors au nombre de quatre, serviraient à repérer les volumes et mettre en place une représentation visuelle de la profondeur.
Le croquis ci-dessous reprend les quatre types de jonctions :
1) La marque à l'évidence les angles droits, y compris lorsque ceux-ci sont perçus sous un angle de vision qui les déforme. Ainsi, en dépit du raccourci que les lois de la perspective lui imposent, le sommet arrière droit du cube, qui n'a pas été noté comme tel sur le croquis, doit sans doute être considéré comme une jonction en L, en L couché.
2) La illustre la jonction plus ou moins orthogonale de deux surfaces. À ce titre la base avant gauche du cube est aussi une jonction en L.
3) La représente quant à elle le point de rencontre des trois faces d'un volume. Ce qui pour un cube est paradoxalement le maximum de cotés d'un cube que le système perceptif humain est à même d'appréhender à partir d'un point de vue fixe. Se pose alors la question de la jonction en T.
4) La ne sert pas à repérer les volumes. Sa fonction est de mettre en évidence un certains type de relation spatiale : le recouvrement. En cela, elle nécessite la présence de deux éléments distincts échelonnés dans l'espace, que ces derniers soient des volumes ou des surfaces, tandis que les jonctions précédentes se suffisaient d'un seul volume ou d'une seule surface.
À partir de ce savoir issu de la recherche en psychologie de la perception, nous allons essayer de voir si la Classification toujours perfectible des figures impossibles et ambiguës, classification plastique et non perceptive, n'aurait pas, en dépit de sa plasticité, quelques points communs avec la théorie des jonctions.

LA SUPERPOSITION ÉQUIVOQUE ET LES JONCTIONS EN FLÈCHE ET EN Y
LE DIÈDRE DE MACH
Si les jonctions permettent, en l'état actuel de la connaissance, d'expliquer le travail opéré par le système perceptif pour aboutir à une reconstruction tridimensionnelle du monde, certaines illusions connues mettent à mal ce processus. Nous allons commencer par le Dièdre de , qui, en tant que figure réversible, donne lieu à une ambiguïté du convexe et du concave. Avec cette figure, nous pourrions croire à une remise en cause des jonctions en flèche et en Y.
Dans un premier temps, j'ai toujours pensé que nous avions là une ambiguïté d'orientation de la verticale médiane (voir Tableau n°19). Cette dernière pouvant tout autant être comprise comme une ligne qui se dresse vers le ciel pour former un livre ouvert, que comme une horizontale qui fuit, parallèle au sol, pour exprimer le faîte d'une tente. Bien que les deux tracés angulaires qui lui sont associés (croquis ci-dessous à droite) ne passent pas de l'obtus à l'aigu et inversement, leur orientation est bien modifiée. Mais, il semble que ces deux éléments ne soient pas essentiels en ce qu'ils ne font qu'accompagner le changement de direction de l'ensemble des lignes de cette figure qui voient leur orientation modifiée. Si les jonctions en flèche et en Y marquent et indiquent des angularités, elles n'ont donc pas pour objet d'attribuer une orientation univoque aux angles qu'elles désignent., ouvrant ainsi la porte à une équivoque du convexe et du concave.
Les jonctions étant innocentées, nous pouvons supposer que l'absence de contexte est à l'origine de la réversibilité du Dièdre. Bizarrement, en cette figure, ce n'est pas le plan du sol qui, en tant que contexte, fait défaut. Nous pourrions tout aussi bien avoir un livre ouvert posé dans l'herbe qu'une tente montée dans une salle d'exposition. Ici, les éléments contextuels manquants sont donc les détails appartenant aux deux objets en conflit. En cela, ce type de figure réversible ne devrait pas avoir sa place dans le réel qui présente toujours un contexte fort et riche en détails. Nous verrons pourtant que cette superposition équivoque de deux formes aux orientations contraires peut être trouvée à l'état naturel.
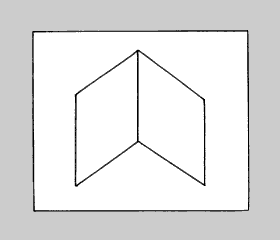  
LE CUBE DE NECKER
Encore une fois, ce ne sont ni la pointe de la flèche, ni la fourche du Y qui ici sont ambiguës puisque toutes deux signifient bien l'angle du cube. Ce sont toutes les lignes qui, en modifiant leur échelonnement pour les unes et leur orientation pour les autres, en arrivent à cette figure ambiguë. Mais ici, la réversibilité est différente en ce que nous n'avons plus à hésiter entre le concave et le convexe, mais sommes confrontés à deux points de vue antagoniques sur un même volume : la plongée et la contre-plongée. Ainsi et encore une fois, les jonctions en flèche et en Y, qui indiquent les angularités, n'ont pas pour fonction d'imposer un point de vue univoque sur les angles qu'elles expriment, ouvrant alors la porte à une équivoque de la plongée et de la contre-plongée.
Les jonctions étant une nouvelle fois innocentées, nous pouvons encore supposer que l'absence de contexte est à l'origine de la réversibilité du Cube. Mais cette fois, nous pouvons incriminer l'absence du plan du sol qui, en tant que contexte, fait bien défaut. Sans lui, nous ne saurons jamais si ce volume est posé à terre ou vole dans les airs. En cela, cet autre type de figure réversible ne devrait pas avoir sa place dans le réel et cette superposition équivoque d'une forme sur laquelle nous portons deux points de vue différents ne m'est pas encore apparue à l'état naturel. Passons justement au réel, ou, pour le moins, à quelques unes de ses représentations photographiques.
  
L'OMBRE DE LA POUBELLE
Mais le réel peut se révéler, à la fois tout aussi simple et beaucoup plus complexe que le dessin. Avec cette photo nous avons une figure dont la réversibilité est devenue tellement inégale que nous croyons, tout d'abord, voir en cette ombre portée une forme pleine (un tabouret) en lieu et place de l'objet creux (la poubelle). Il est vrai que nous sommes ici dans un réel graphique où les ombres dessinent à la surface du sol qui leur sert de feuillet. Mais, à retourner la photo, les jonctions en flèche et en Y peuvent donner lieu aux deux interprétations du Dièdre de , le concave et le convexe. De même qu'en forçant notre attention, nous pouvons, à partir d'une seule photo, passer d'un point de vue en plongée à un autre en contre-plongée, comme avec le Cube de . Passons alors à un réel en trois dimensions.
Pour une autre analyse de cette image, voir : Objet renversant.
  
GARE DE LYON
Avec le "vrai" réel, nous allons trouver de nouvelles failles aux jonctions. Ainsi, lorsque la photographie de ces immeubles de bureau situés près de la gare de Lyon est sous exposée (ci-dessous à gauche), nous pouvons croire à la présence d'une tour supplémentaire. Le fait est que l'angle obtus formé par la pointe de l'ombre évoque à s'y méprendre une jonction en flèche (tracé rouge) qui, pour notre système perceptif, évoque habituellement la présence d'un volume, ou, pour le moins, une angularité. C'est ainsi qu'une jonction peut en arriver à trahir nos attentes dans le réel. Mais, à la différence des figures réversibles vues précédemment, notre perception hésite ici entre la platitude de l'ombre et la volumétrie d'un supposé immeuble.
Il apparaît ainsi que les jonctions en flèche et en Y en arrivent parfois à trahir notre perception du réel. Avec elles, des angularités planes peuvent devenir des angularités de volumes. C'est alors que deux interprétations se succèdent, qui nous amènent à retrouver dans la graphie du réel, les superpositions équivoques des dessins.
Pour une analyse plus complète de cette image, voir : Gare de Lyon.
  
L'ALIGNEMENT ÉQUIVOQUE ET LES JONCTIONS EN L
Les jonctions en L ont une fonction simple qui est de nous informer de la présence d'une orthogonalité, quand bien même, celle-ci, vue en perspective, en arriverait à perdre l'orthogonalité graphique du L. Mais, là encore, les jonctions échouent parfois dans leur mission perceptive. Ainsi, le tracé rouge ajouté au dessin présenté ci-dessous peut expliquer la raison pour laquelle nous avons tendance à voir là un carré rempli de poutres : trois barres en lévitation sur la gauche du croquis. Mais, il aurait encore été possible d'ajouter un L renversé rouge dans le coin supérieur droit, afin d'expliquer la lévitation du coté droit de cet illusoire carré.
Une fois encore, il est à remarquer que les jonctions échouent à nous donner les orientations des angularités qu'elles expriment. Nous avons bien un L en cette image, si ce n'est que ce L ne se dresse pas fièrement devant nous à la verticale, mais s'éloigne au sol et que son véritable tracé ne peut être perçu que du ciel. C'est sans doute en cela que nous faisons léviter ces barres dans l'image, afin de ne pas avoir à léviter pour les voir telles qu'elles devraient être dans le réel.
Quoiqu'il en soit, l'alignement plastique des deux bords verticaux de ce carré apparent suffisent déjà à expliquer la lévitation illusoire, sans que nous ayons à convoquer les jonctions en L. Nous sommes là dans l'équivoque d'orientation des lignes verticales vue plus haut (pour une autre interprétation voir : Croquis 37b2). Voyons maintenant si le réel peut prêter à la même confusion.
  
PALAIS DE TOKYO
Avec les marches du , les L réels de la construction disparaissent parfois, échouant alors à nous indiquer l'angularité du plan incliné que nous avons à gravir. C'est que le coté gauche de l'ombre portée de la colonne, qui devrait reproduire presque à l'identique la successivité des L des marches, est perçu sous un point de vue tel qu'il aligne ses différents segments sur une oblique continue et surtout illusoire. Nous en arrivons au paradoxe suivant : alors que les jonctions en flèche et en Y laissaient parfois croire à la présence de volumes inexistants, la jonction en L peut disparaître pour indiquer l'absence de volumes existants. Pour une autre analyse de cette photo, voir : Aux marches du Palais.
Pour lors, passons à une autre photo pour voir les effets des jonctions en L dans le réel.
  
CHEMINÉES
Ces conduits de fumée vous ont des airs d'immenses clés coudées (ci-dessous à gauche). Pourtant, lorsque vous les contemplez d'un autre point de vue (ci-dessous à droite), vous devrez vous rendre à l'évidence : ce qui apparaissait comme étant des plans pliés à angle droit ne sont plus que des lignes brisées parallèles disposées à l'intérieur d'un seul et même plan. C'est ainsi que les soi-disants L répétés des conduits vous ont encore une fois induit en erreur. Alors que le point de vue sur l'ombre de la colonne faisait disparaître les L réels marquant les angles des marches, cet autre point de vue affiche des L illusoires qui donnent à voir des angularités inexistantes. Tout ici est donc affaire de point de vue. Pour un autre point de vue sur ces mêmes photos, voir : Cheminées.
Nous allons maintenant aborder les jonctions en T.
  
LE CONTACT ÉQUIVOQUE ET LES JONCTIONS EN T
LES DEUX POLYGONES
Les jonctions en T ont une fonction simple qui est de nous informer du recouvrement d'une forme par une autre. Mais, comme nous allons le voir, si ces jonctions parviennent à signifier l'ordre des plans, elles s'arrêtent là et peuvent même échouer devant cette tâche simple. Pire encore, elles ne vont pas jusqu'au bout de leur mission perceptive, incapables qu'elles sont de nous informer des distances et des écarts. Pour cela d'autres mécanismes, de plus haut niveau, doivent sans doute prendre le relais.
Ainsi, alors que nous percevons bien l'ordre des plans des Deux Polygones(ci-dessous à gauche), nous sommes dans l'incapacité d'évaluer la distance qui les sépare. Nous pourrions invoquer, comme pour le Dièdre de , l'absence de contexte (plan du sol). Mais, comme nous le verrons plus loin, même un contexte réaliste n'arrive pas à donner un échelonnement juste et précis des éléments en présence. Les jonctions en T, qui indiquent l'ordre des plans, n'ont pas pour fonction de donner la mesure de l'écart qui les sépare, ouvrant alors la porte à une équivoque que nous qualifierons, faute de mieux, de l'échelonnement.
Enfin, pour couronner le tout, une interprétation formelle échappe aux jonctions en T. Il est possible de voir ou de construire une figure où un L, renversé la tête en bas, serait porté par le rectangle inférieur. Ce même L pourrait encore être situé loin en arrière ou même bien en avant du quadrilatère restant. Car, rien en cette image n'interdit de percevoir la contiguïté réelle ou illusoire de deux formes différentes en lieu et place du recouvrement apparent de deux rectangles.
  
LE T À CONTACT DE CONTOURS
Avec cette figure personnelle (ci-dessus à droite), la jonction en T a été involontairement appliquée à un soi-disant T constitué de deux blocs. Mais, en lieu et place du possible contact équivoque des Deux Polygones précédents, nous avons maintenant une contiguïté ambiguë des contours : les arêtes de ces volumes sont-elle jointes ou disjointes ? Une fois encore, il est à remarquer que les jonctions en T échouent à nous donner les échelonnements des formes qu'elles mettent en contact apparent..
Mais cette fois, nous pouvons véritablement incriminer l'absence de contexte, tant le plan du sol que la présence des ombres portées permettraient ici de résoudre l'équivoque. Sans ces indices, nous ne saurons jamais si la barre horizontale est posée à terre, loin en arrière de la poutre dressée vers le ciel, ou si elle est suspendue dans les airs, fixée à son homologue. En cela, cet autre type de contact ambigu ne devrait pas avoir sa place dans le réel, pour rester confiné à la représentation. Passons maintenant au réel, ou, pour le moins, à quelques unes de ses représentations photographiques afin de vérifier ces hypothèses.
LA CROIX DE VASSIVIÈRE
La croix est posée sur le muret, la croix n'y est plus. Comme avec le dessin du T, la jonction en T hésite entre la contiguïté et l'éloignement. L'ensemble du contexte, le sol, l'herbe, les matières, la lumière et les ombres n'y peuvent rien, l'ambiguïté d'échelonnement persiste dans le réel. Ici, comme dans les photographies précédentes, nous sommes contraints de déplacer le point de vue du regardeur pour nous assurer de la vérité des jonctions, qui subissent de plein fouet les ambiguïtés plastiques, en l'occurrence le contact équivoque. C'est ainsi que les mécanismes perceptifs échouent devant la plasticité de l'image et seul un réel tridimensionnel et surtout mouvant (un réel où l'on peut se déplacer) est à même de résoudre nos interrogations perceptives.
Pour une autre approche de la croix, voir : Vassivière.
  
L'ENSEIGNE QUI VOLE AU VENT
Ces deux photos viennent contredire ce qui vient d'être affirmé. Car, si dans un premier temps, l'enseigne de ce magasin semble flotter au vent du mat situé à sa gauche, après un déplacement de quelques mètres, elle paraît fixé au poteau placé à sa droite. La solution est simple : l'enseigne est plaquée sur la façade de tôle grise, qui donne sur le parking où sont plantés deux réverbères. Nous avons donc là deux jonctions en T successives et illusoires, seule la troisième, unissant le logo à la façade, restera, quelque soit le point de vue, acceptable. Ici encore, le contact équivoque des contours arrive à perturber le rôle des jonctions en T, donnant maintenant lieu à la perception de trois échelonnements réciproques et contradictoires de deux éléments disposés dans la profondeur du réel.
Pour une analyse titubante de ce magasin de banlieue, voir : L'enseigne.
  
CONCLUSION
Au vu des résultats, cet article semble des plus inutiles. Certains auront cependant remarqué que le rôle des jonctions n'est pas aussi important que ce qu'il aurait pu paraître. Indiquer la présence d'un angle ne suffit aucunement à le définir, ni même à prouver son existence. Tandis que le Dièdre de et le Cube de montrent à l'envi que les flèches et les Y ne suffisent pas à définir les orientations, les Deux Polygones et le T prouvent que les jonctions en T échouent à rendre compte des échelonnements. La photographie va plus loin encore, qui, à l'aide des mêmes schémas, nous fait croire à la présence de volumes inexistants (gare de Lyon), à l'aplatissement de volumes existants (Palais de Tokyo) ou au contact d'éléments distants (Croix de Vassivière).
Deux constats sont donc à établir. En premier lieu, les jonctions en flèche et en Y nous signifient la présence de volumes, mais leur mission s'arrête là et elles en arrivent même à échouer devant cette tâche simple (il n'a pas été dit que le Dièdre de pouvait être une forme plane constituée de deux losanges accolés). De plus, elles n'assument pas jusqu'au bout leur mission de rendu des angularités, en ce que les figures réversibles se jouent des flèches et des Y pour donner lieu aux équivoques d'orientations : le passage du concave au convexe, et celui de la plongée à la contre-plongée.
En second lieu, si les jonctions en T nous signifient le recouvrement des plans, leur mission s'arrête là en ce qu'elles échouent parfois devant cette tâche simple (les Deux Polygones). Pire encore, elles ne vont pas jusqu'au bout de leur mission perceptive, incapables qu'elles sont de nous informer des distances et des écarts, ouvrant la porte aux équivoques d'échelonnement. Nous pouvons donc supposer que d'autres mécanismes doivent prendre le relais afin de terminer le travail ébauché par les jonctions. Mécanismes qui doivent être de plus haut niveau, en ce que leur tâche s'avère des plus ardues : attribuer une orientation unique à chaque contour et définir l'échelonnement réciproque des différentes surfaces.
Il n'en reste pas moins que la théorie des jonctions s'accommode fort bien des trois principes plastiques défendus ici. Tandis que la superposition équivoque marque les limites des jonctions en flèche et en Y, l'alignement ambigu s'attaque aux jonctions en L et le contact illusoire perturbe le bon fonctionnement des jonctions en T. Si les lois de la perception n'épousent sans doute pas terme à terme les lois d'élaboration plastique de l'image, certaines convergences peuvent être décelées, qui sont communes à ces deux systèmes, l'un de perception de la chose vue, l'autre de fabrication de la chose à percevoir. Avec ces trois principes plastiques, nous atteignons le juste milieu : le moment médian, toujours là, à jamais fixé sur le papier, qu'il soit à dessin ou photographique, qui attend la venue d'une paire de globes oculaires pour qu'enfin se révèle, à l'intérieur d'un cerveau sûr de lui et du monde sur lequel reposent ses pieds, la vanité de toute perception, l'illusion des images et l'insignifiance de nos attentes.
BIBLIOGRAPHIE
La reconnaissance des objets, coll. La Psychologie en plus, Presses Universitaires de Grenoble, Grenoble, 1996.
RETOUR AU SOMMAIRE ARTICLES
RETOUR AU SOMMAIRE THÉORIE
RETOUR À L'ACCUEIL
|
|





















